Problemas de lógica
1)
Três sábios iriam participar de um concurso para ver quem era mais
sábio. O rei da região pegou cinco faixas de pano, três brancas e duas
pretas. Três das cinco faixas seriam entregues aleatoriamente aos
sábios, sem que eles vissem a cor, e seriam amarradas na testa de cada
um deles. O primeiro sábio veria as cores das faixas dos outros dois,
e tentaria adivinhar sua própria cor. O segundo veria a cor do
terceiro e, sabendo se o primeiro errou ou não (mas sem saber qual foi
o chute dele), tentaria adivinhar a própria cor. O terceiro, não veria
nada, mas saberia se os dois primeiros acertaram ou não (sem saber
também quais foram os chutes).
Chega o primeiro sábio, e após ver as duas outras cores escreveu ao
rei qual era sua cor. O rei anuncia em voz alta: O primeiro sábio
acaba de errar!
O segundo sábio olha a cor da faixa do terceiro, e escreve ao rei qual
seria a própria cor. O rei: O segundo sábio errou!
O terceiro sábio escreve ao rei sua cor. E o rei: O terceiro sábio
acertou!
Como ele acertou?
2)
Uma pessoa está diante de duas portas, uma que a leva à salvação, e
outra a leva à morte. Cada porta tem um guardião, que sabe o que há
atrás da porta. Um dos guardiões somente fala a verdade, e o outro
somente mentiras, e a pessoa sabe disso, mas não sabe quem é quem. Os
guardiões respondem apenas sim ou não, e se não souberem a resposta de
alguma pergunta que foi feita a eles, ficam furiosos e matam quem fez
a pergunta. A pessoa tem que passar por uma das portas, e tem direito
a apenas uma pergunta para um dos guardiões. Cada guardião não sabe se
o outro fala verdades ou mentiras, apenas a pessoa sabe disso.
Qual a pergunta que a pessoa deve fazer para que possa ter certeza que
vai sair salva?
3)
Um torcedor do time X encontra-se com três jogadores após um jogo. Um
é o zagueiro, um é o atacante, e o outro um meio-campista. O meio
campista fala mentiras e verdades, o atacante apenas mente, e o
zagueiro fala somente a verdade, e o torcedor sabe disso. Mas o
torcedor conhece apenas o meio-campista, não sabe quem é o atacante ou
zagueiro. O torcedor pergunta:
- Qual foi o resultado do jogo?
Um deles responde:
- Empatamos.
O outro:
- Não empatamos.
E o terceiro:
- Perdemos.
Nisso o torcedor, que era muito inteligente, fala:
- Ah, já sei qual o resultado!
Quem falou o que? Qual o resultado do jogo?
4)
Três padres e três índios estão na margem de um rio, e querem
atravessá-lo usando uma canoa que agüenta apenas duas pessoas. Os
índios são antropófagos, de forma que os padres nunca podem estar em
menor número, seja em uma das margens do rio, seja no embarque ou
desembarque. Como eles devem fazer para atravessar o rio?
5)
Tenho doze bolinhas esféricas aparentemente iguais, mas sei que uma
delas tem peso diferente das outras. Utilizando uma balança comum de
dois pratos (aquela que apenas compara dois pesos diferentes), como
posso descobrir qual é a bolinha diferente, com no máximo três
pesagens?
6)
Einstein escreveu esse teste no século passado. Ele disse que 98% do
mundo não pode resolvê-lo!
1. Há cinco casas de 5 diferente cores.
2. Em cada casa mora uma pessoa de diferente nacionalidade.
3. Esses cinco proprietários bebem diferentes bebidas, fumam
diferentes tipos de cigarro e também têm um certo animal de estimação.
4. Nenhum deles tem o mesmo animal, fuma o mesmo cigarro ou bebe a
mesma bebida.
Dicas:
1. O inglês vive na casa vermelha.
2. O sueco tem um cachorro como animal de estimação.
3. O dinamarquês bebe chá.
4. A casa verde fica à esquerda da casa branca.
5. O dono da casa verde bebe café.
6. A pessoa que fuma Pall Mall cria pássaros.
7. O dono da casa amarela fuma Dunhill.
8. O homem que vive na casa do centro bebe leite.
9. O norueguês vive na primeira casa.
10. O homem que fuma Blends vive ao lado do que tem gatos.
11. O homem que cria cavalos vive ao lado do que fuma Dunhill.
12. O homem que fuma Bluemaster bebe cerveja.
13. O alemão fuma Prince.
14. O norueguês vive ao lado da casa azul.
15. Uma das pessoas bebe água.
[A última dica foi modificada pois era redundante]
Quem tem um peixe ?
7)
Há três cartas viradas sobre uma mesa. Sabe-se que em cada uma delas
está escrito um número inteiro positivo. São dadas a Carlos, Samuel e
Tomas as seguintes informações:
1) todos os números escritos nas cartas são diferentes
2) a soma dá 13
3) os números estão em ordem crescente da esquerda à direita
Primeiro, Carlos olha o número da carta da esquerda e diz: "Não tenho
informações suficientes para determinar os outros dois números". Em
seguida, Tomas olha o número na carta da direita e diz: "Não tenho
informações suficientes para determinar os dois outros números". Por
fim, Samuel olha a carta do meio e diz "Não tenho informações
suficientes para determinar os dois outros números". Sabendo que cada
um deles sabe que os outros dois são inteligentes e escuta os
comentários dos outros, qual é o numero da carta do meio?
8)
Mil armários estão enfileirados e numerados (1, 2, 3, 4, ...), mil
alunos também numerados de 1 a 1000, começam a seguinte brincadeira: o
1º aluno passa por todos os armários (que inicialmente estavam
fechados) e abre suas portas; o 2º aluno passa por todos os armários e
inverte as posições das portas 2, 4, 6, 8, ...; o 3º aluno passa por
todos os armários e inverte as posições das portas 3, 6, 9, 12, ... E
assim sucessivamente, isto é, cada aluno que passa inverte as posições
dos armários que têm números múltiplos do seu próprio número. Após os
mil alunos passarem, quantos armários permanecem abertos?
9)
Dez cientistas participam de um projeto secreto. Devido à grande
importância do projeto, as pessoas só podem ter acesso aos arquivos
quando há pelo menos cinco cientistas presentes. Para isso, foram
utilizados diversos cadeados que trancam o acesso à sala da pesquisa.
Quantos cadeados são necessários? Quantas chaves devem ser entregues
para cada cientista?
10)
Há em uma mesa 100 cartas numeradas de 1 até 100. Cada carta de número
n, contém a afirmação "Há n cartas falsas na mesa". Quantas cartas
verdadeiras há na mesa?
11)
Há em uma mesa 100 cartas numeradas de 1 até 100. Cada carta de número
n, contém a afirmação "Há pelo menos n cartas falsas na mesa". Quantas
cartas verdadeiras há na mesa?
12)
Há um número de 10 algarismos em que a primeira posição representa a
quantidade de algarismos 0 desse número, a segunda posição representa
a quantidade de algarismos 1 desse numero, e assim por diante, até a
décima posição, que representa a quantidade de algarismos 9 do número.
Qual é esse número?
Desafio: No problema anterior, foi utilizado o sistema de numeração
decimal. Em uma base n diferente de 10, o problema pode não ter
solução, ao se procurar um número em que cada algarismo represente a
quantidade de algarismos de 0 até n-1. Pode também ter mais de uma
solução. Quais são as bases numéricas em que o problema não tem
solução? Em quais bases há mais de uma solução?
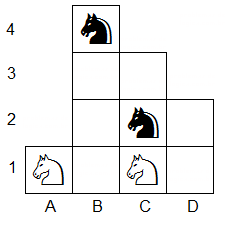
13)
Imagine que o desenho abaixo é um pedaço de tabuleiro de xadrez. Quais
movimentos devem ser feitos para trocar as posições dos cavalos
brancos com as dos pretos, usando apenas as casas desenhadas?
 14)
As galinhas de penacho dourado
Era uma vez um galinheiro muito curioso. Todas as galinhas possuíam um
lindo penacho dourado, o que era motivo de muito orgulho para elas.
Tanto que, se alguma galinha descobre que perdeu seu maravilhoso
penacho, no mesmo dia que ela descobre ela se mata. Mas só se mata à
meia-noite, em um horário em que geralmente as galinhas estão
dormindo.
Porém, descobrir que perdeu o penacho pode levar muito tempo. Elas não
conseguem olhar para o próprio penacho e não se comunicam de forma
alguma uma com a outra. Mas são inteligentíssimas. O brilhante
raciocínio lógico que elas têm é a única maneira delas descobrirem que
perderam o penacho (pobres galinhas, se não fossem tão inteligentes
viveriam mais).
Certo dia, Tio Patinhas descobre esse galinheiro. Ganancioso como ele
é, já pensa em ganhar dinheiro com esses penachos. Chama seu sobrinho,
o Pato Donald, e o manda roubar alguns penachos. Assim ele faz.
Enquanto todas as galinhas dormiam, sem que ninguém percebesse, o
malvado roubou os penachos de sete galinhas. Mas na fuga, com medo que
alguém acordasse, deixou cair um penacho, que ficou no meio do
galinheiro.
Passados alguns dias, todas as galinhas que perderam o penacho se
matam, numa mesma noite. Pergunta: quantos dias se passaram e como
elas descobriram?
15)
Tenho três baldes sem graduação, com capacidades para 8, 5 e 3 litros.
Começando com o balde de 8 litros cheio e os outros vazios, como
separar 4 litros em dois dos baldes?
16)
Com uma ampulheta de 7 minutos e outra de 11, como marcar 15 minutos?
17)
Existem duas caixas, "A" e "B". Um aviso na caixa A diz "O aviso na
caixa B é verdadeiro e o ouro está na caixa A". Um aviso na caixa B
diz "O aviso na caixa A é falso e o ouro está na caixa A". Assumindo
que existe ouro em uma das caixas, qual delas contém o ouro?
18)
Tenho uma balança de dois pratos (balança que compara pesos), e quero
ser capaz de pesar objetos de 1 até 40 kg, com precisão de 1 kg. Para
isso serão usados 4 pesos. Quanto pesará cada um deles?
19)
Você tem dez pilhas de moedas com nove moedas em cada pilha. Cada
moeda pesa 10g com exceção das moedas de uma única pilha que pesam 9g
cada. Como descobrir qual a pilha em que as moedas pesam 9g usando,
para isso, uma balança de supermercado (balança com graduação) uma
única vez?
14)
As galinhas de penacho dourado
Era uma vez um galinheiro muito curioso. Todas as galinhas possuíam um
lindo penacho dourado, o que era motivo de muito orgulho para elas.
Tanto que, se alguma galinha descobre que perdeu seu maravilhoso
penacho, no mesmo dia que ela descobre ela se mata. Mas só se mata à
meia-noite, em um horário em que geralmente as galinhas estão
dormindo.
Porém, descobrir que perdeu o penacho pode levar muito tempo. Elas não
conseguem olhar para o próprio penacho e não se comunicam de forma
alguma uma com a outra. Mas são inteligentíssimas. O brilhante
raciocínio lógico que elas têm é a única maneira delas descobrirem que
perderam o penacho (pobres galinhas, se não fossem tão inteligentes
viveriam mais).
Certo dia, Tio Patinhas descobre esse galinheiro. Ganancioso como ele
é, já pensa em ganhar dinheiro com esses penachos. Chama seu sobrinho,
o Pato Donald, e o manda roubar alguns penachos. Assim ele faz.
Enquanto todas as galinhas dormiam, sem que ninguém percebesse, o
malvado roubou os penachos de sete galinhas. Mas na fuga, com medo que
alguém acordasse, deixou cair um penacho, que ficou no meio do
galinheiro.
Passados alguns dias, todas as galinhas que perderam o penacho se
matam, numa mesma noite. Pergunta: quantos dias se passaram e como
elas descobriram?
15)
Tenho três baldes sem graduação, com capacidades para 8, 5 e 3 litros.
Começando com o balde de 8 litros cheio e os outros vazios, como
separar 4 litros em dois dos baldes?
16)
Com uma ampulheta de 7 minutos e outra de 11, como marcar 15 minutos?
17)
Existem duas caixas, "A" e "B". Um aviso na caixa A diz "O aviso na
caixa B é verdadeiro e o ouro está na caixa A". Um aviso na caixa B
diz "O aviso na caixa A é falso e o ouro está na caixa A". Assumindo
que existe ouro em uma das caixas, qual delas contém o ouro?
18)
Tenho uma balança de dois pratos (balança que compara pesos), e quero
ser capaz de pesar objetos de 1 até 40 kg, com precisão de 1 kg. Para
isso serão usados 4 pesos. Quanto pesará cada um deles?
19)
Você tem dez pilhas de moedas com nove moedas em cada pilha. Cada
moeda pesa 10g com exceção das moedas de uma única pilha que pesam 9g
cada. Como descobrir qual a pilha em que as moedas pesam 9g usando,
para isso, uma balança de supermercado (balança com graduação) uma
única vez?
 14)
As galinhas de penacho dourado
Era uma vez um galinheiro muito curioso. Todas as galinhas possuíam um
lindo penacho dourado, o que era motivo de muito orgulho para elas.
Tanto que, se alguma galinha descobre que perdeu seu maravilhoso
penacho, no mesmo dia que ela descobre ela se mata. Mas só se mata à
meia-noite, em um horário em que geralmente as galinhas estão
dormindo.
Porém, descobrir que perdeu o penacho pode levar muito tempo. Elas não
conseguem olhar para o próprio penacho e não se comunicam de forma
alguma uma com a outra. Mas são inteligentíssimas. O brilhante
raciocínio lógico que elas têm é a única maneira delas descobrirem que
perderam o penacho (pobres galinhas, se não fossem tão inteligentes
viveriam mais).
Certo dia, Tio Patinhas descobre esse galinheiro. Ganancioso como ele
é, já pensa em ganhar dinheiro com esses penachos. Chama seu sobrinho,
o Pato Donald, e o manda roubar alguns penachos. Assim ele faz.
Enquanto todas as galinhas dormiam, sem que ninguém percebesse, o
malvado roubou os penachos de sete galinhas. Mas na fuga, com medo que
alguém acordasse, deixou cair um penacho, que ficou no meio do
galinheiro.
Passados alguns dias, todas as galinhas que perderam o penacho se
matam, numa mesma noite. Pergunta: quantos dias se passaram e como
elas descobriram?
15)
Tenho três baldes sem graduação, com capacidades para 8, 5 e 3 litros.
Começando com o balde de 8 litros cheio e os outros vazios, como
separar 4 litros em dois dos baldes?
16)
Com uma ampulheta de 7 minutos e outra de 11, como marcar 15 minutos?
17)
Existem duas caixas, "A" e "B". Um aviso na caixa A diz "O aviso na
caixa B é verdadeiro e o ouro está na caixa A". Um aviso na caixa B
diz "O aviso na caixa A é falso e o ouro está na caixa A". Assumindo
que existe ouro em uma das caixas, qual delas contém o ouro?
18)
Tenho uma balança de dois pratos (balança que compara pesos), e quero
ser capaz de pesar objetos de 1 até 40 kg, com precisão de 1 kg. Para
isso serão usados 4 pesos. Quanto pesará cada um deles?
19)
Você tem dez pilhas de moedas com nove moedas em cada pilha. Cada
moeda pesa 10g com exceção das moedas de uma única pilha que pesam 9g
cada. Como descobrir qual a pilha em que as moedas pesam 9g usando,
para isso, uma balança de supermercado (balança com graduação) uma
única vez?
14)
As galinhas de penacho dourado
Era uma vez um galinheiro muito curioso. Todas as galinhas possuíam um
lindo penacho dourado, o que era motivo de muito orgulho para elas.
Tanto que, se alguma galinha descobre que perdeu seu maravilhoso
penacho, no mesmo dia que ela descobre ela se mata. Mas só se mata à
meia-noite, em um horário em que geralmente as galinhas estão
dormindo.
Porém, descobrir que perdeu o penacho pode levar muito tempo. Elas não
conseguem olhar para o próprio penacho e não se comunicam de forma
alguma uma com a outra. Mas são inteligentíssimas. O brilhante
raciocínio lógico que elas têm é a única maneira delas descobrirem que
perderam o penacho (pobres galinhas, se não fossem tão inteligentes
viveriam mais).
Certo dia, Tio Patinhas descobre esse galinheiro. Ganancioso como ele
é, já pensa em ganhar dinheiro com esses penachos. Chama seu sobrinho,
o Pato Donald, e o manda roubar alguns penachos. Assim ele faz.
Enquanto todas as galinhas dormiam, sem que ninguém percebesse, o
malvado roubou os penachos de sete galinhas. Mas na fuga, com medo que
alguém acordasse, deixou cair um penacho, que ficou no meio do
galinheiro.
Passados alguns dias, todas as galinhas que perderam o penacho se
matam, numa mesma noite. Pergunta: quantos dias se passaram e como
elas descobriram?
15)
Tenho três baldes sem graduação, com capacidades para 8, 5 e 3 litros.
Começando com o balde de 8 litros cheio e os outros vazios, como
separar 4 litros em dois dos baldes?
16)
Com uma ampulheta de 7 minutos e outra de 11, como marcar 15 minutos?
17)
Existem duas caixas, "A" e "B". Um aviso na caixa A diz "O aviso na
caixa B é verdadeiro e o ouro está na caixa A". Um aviso na caixa B
diz "O aviso na caixa A é falso e o ouro está na caixa A". Assumindo
que existe ouro em uma das caixas, qual delas contém o ouro?
18)
Tenho uma balança de dois pratos (balança que compara pesos), e quero
ser capaz de pesar objetos de 1 até 40 kg, com precisão de 1 kg. Para
isso serão usados 4 pesos. Quanto pesará cada um deles?
19)
Você tem dez pilhas de moedas com nove moedas em cada pilha. Cada
moeda pesa 10g com exceção das moedas de uma única pilha que pesam 9g
cada. Como descobrir qual a pilha em que as moedas pesam 9g usando,
para isso, uma balança de supermercado (balança com graduação) uma
única vez?